3.11 Силы,
действующие в зубчатом зацеплении
Для расчета валов, осей и их опор необходимо определить силы, возникающие в
зубчатом зацеплении. Если пренебречь силами трения в зацеплении, то можно
считать, что вектор суммарного усилия Q взаимодействия между зубьями лежит на
линии зацепления (она же общая нормаль к профилям зубьев), проходящей через
полюс зацепления перпендикулярно профилям зубьев.
1. Прямозубое цилиндрическое зацепление
Нормальное усилие Q (рисунок 3.17, а) раскладываем на составляющие - окружное
усилие Р и радиальное (распорное) усилие Т.
Окружное усилие
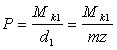 ,
распорное усилие Т = P•tgα.. ,
распорное усилие Т = P•tgα..
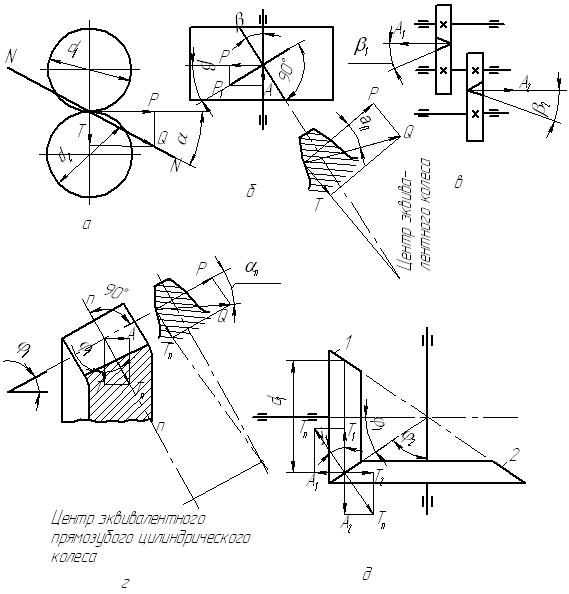
Рисунок 3.17 - Силы, действующие в зубчатом
зацеплении
Просмотреть ближе
2. Косозубое цилиндрическое зацепление
Нормальное усилие Q (рисунок 3.17, б), действующее в плоскости зацепления,
раскладываем на две составляющие — радиальное (распорное) усилие Т и окружное
усилие Р1, действующее в плоскости зацепления. В свою очередь усилие
P1 разложим на две составляющие — окружное усилие Р, действующее в
торцевой плоскости, и осевое усилие А.
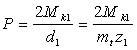 ,
А = Ptgβ, ,
А = Ptgβ,
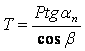 . .
С увеличением угла наклона зубьев β осевая сила А также увеличивается, что
вызывает дополнительные нагрузки. Поэтому обычно ограничивают углы β = 8÷25°.
В том случае, когда на одном валу находятся два косозубых колеса (рисунок
3.17, в), для уравновешивания осевых усилий направление зубьев этих колес должно
быть одинаковым, а углы наклона зубьев различны с тем чтобы можно было достичь
равенства А1 =А2. С этой целью одним из углов задаемся,
например β1 , а другой вычисляем из условия уравновешивания осевой
нагрузки.
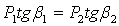 ,
отсюда ,
отсюда
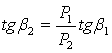 . .
Однако следует иметь в виду, что межосевое расстояние при этом может быть
выражено дробным числом, что усложняет измерения. Этого можно избежать
посредством зубчатых колес со смещением, допустимого отклонения в передаточном
числе и соответствующего подбора углов наклона зубьев β.
3. Прямозубое коническое зацепление
Силу Q, нормальную к профилю зуба эквивалентного цилиндрического колеса,
действующую вдоль линии зацепления эквивалентной передачи (рисунок 3.17, г),
условно считаем приложенной в среднем сечении зубьев колеса (это сечение
нормально к образующим начального конуса) и раскладываем на две составляющие:
окружное усилие
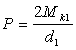 ,
где ,
где
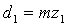 , ,
и распорное Тn , раздвигающее зубья колес в плоскости п
- п,
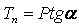
В свою очередь Тn разложим на две составляющие: осевую А и
радиальную силу Т.
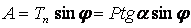 ; ;
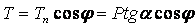 . .
Из рассмотрения рисунке 3.17, д следует, что при межосевом угле φ1 +
φ2 = 90° осевая сила на шестерне равна радиальной на колесе и
радиальная на шестерне равна осевой на колесе.
Поэтому
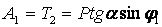
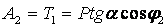 . .
Осевые составляющие силы, дополнительно нагружающие валы и опоры колес,
всегда направлены в сторону больших оснований колес.
4 Конические передачи с косыми и криволинейными
зубьями (рисунок 3.18)
Окружное усилие
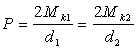 . .
Осевое усилие
|
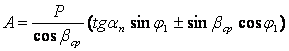 . . |
(30) |
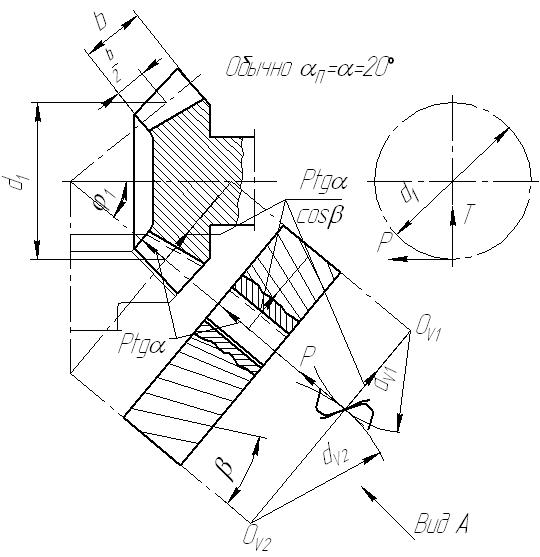
Рисунок 3.18 - Силы, действующие в коническом
непрямозубом зацеплении
Просмотреть ближе
Радиальная сила
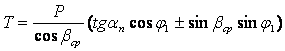 .
Для косозубых конических колес .
Для косозубых конических колес
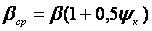
где βср - угол наклона линии зуба к образующей делительного
конуса;
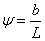 -
степень полноты зуба; -
степень полноты зуба;
b - длина зуба;
L - конусное расстояние.
Знаки при определении усилий А и Т определяются по таблица
3.5:
Таблица 3.5 - Определение знака в уравнениях (30) и (31)
|
Направление |
Знак при втором слагаемом |
|
момента, действующего на
рассматриваемое колесо |
линии зуба |
Уравнение (30) |
Уравнение (31) |
|
По часовой стрелке
Против часовой стрелки |
Правое
Левое
Правое
Левое |
-
+
+
- |
-
+
-
+ |
|
Положительное направление момента указано на рисунке
3.18. Если осевое усилие А окажется отрицательным, то это значит, что оно
направлено не в сторону большего основания колеса, а в противоположную сторону к
вершине конуса, что не желательно по той причине, что возможно заклинивание
передачи при больших зазорах в подшипниках.
|