7.1.4.5 Расчет
числа зубьев зубчатых передач
Для того, чтобы получать группы передач минимального
радиального размера, необходимо найти в каждой группе шестерни с минимальным
числом зубьев, а затем
уже, ориентируясь на это число
зубьев, подобрать число зубьев всех остальных шестерен по передаточным
отношениям.
Так как
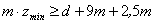
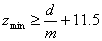 , ,
где
d,
m
– диаметр вала и модуль насаживаемой на него шестерни, мм.
Для группы
i1
– i2
– i3
 .
Принимаем
zmin
= 22. .
Принимаем
zmin
= 22.
Для группы
i4
– i5
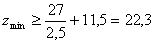 .
Принимаем
zmin
= 23. .
Принимаем
zmin
= 23.
Для группы
i6
– i7
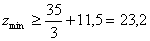 .
Принимаем
zmin
= 24. .
Принимаем
zmin
= 24.
Для группы
i8
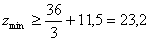 .
Принимаем
zmin
= 24. .
Принимаем
zmin
= 24.
Для группы
i9
 .
Принимаем
zmin
= 25. .
Принимаем
zmin
= 25.
После этого можно приступить к
расчету чисел зубьев всех шестерен привода, пользуясь методом наименьшего
кратного 2 для получения наименьших радиальных размеров привода. Выразим
передаточные отношения в виде простых дробей:
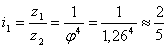 ; ;
 ; ;
 ; ;
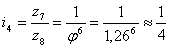 ; ;
 ; ;
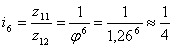 ; ;
 ; ;
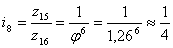 ; ;
 . .
Для ведущих шестерен
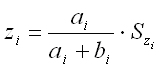 . .
Для ведомых шестерен
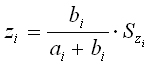 , ,
где
SZi
–
наименьшее кратное
ai
+ bi
для каждой группы передач.
ai,
bi
– целые числа,
выражающие передаточные отношения.
Например, для
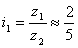 ai
= 2 bi
= 5
ai
= 2 bi
= 5
Для группы передач
i1
– i2
– i3:
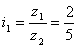 ;
ai + bi = 2+5 = 7; ;
ai + bi = 2+5 = 7;
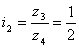 ;
ai + bi = 1+2 = 3; ;
ai + bi = 1+2 = 3;
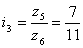 ;
ai + bi = 7+11 = 18; SZi = 7 ∙
18 = 126; ;
ai + bi = 7+11 = 18; SZi = 7 ∙
18 = 126;
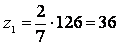 ; ;
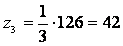 ; ;
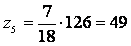 ; ;
 ; ;
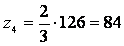 ; ;
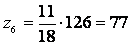 ; ;
Так как
Zmin
для данной группы
передач равно 22 и принимая во внимание, что разница в соседних числах зубьев
тройного блока должна быть не менее 4-5 для беспрепятственного переключения
блока, берем общий делитель 1,5
Тогда
z1
= 23,4
z3 =
28
z5
= 32,7
z2
= 60
z4 = 56
z6
= 51,4
Числа зубьев некоторых шестерен получились дробными, поэтому
для уменьшения погрешности передаточного отношения отбрасываем дробную часть и
получаем:
z1
= 24
z3 = 28
z5
= 32
z2
= 60
z4 = 56
z6
= 51 и
Sz
= 84
Для зубчатой пары
z5-z6
необходимо сделать высотную коррекцию для того, чтобы ее межцентровое расстояние
было равным межцентровому расстоянию зубчатых пар
Для группы передач
i4-i5:
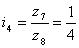 ai + bi = 1+4 = 5
ai + bi = 1+4 = 5
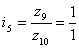 ai + bi = 1+1 = 2 SZi = 2 ∙
5 = 10
ai + bi = 1+1 = 2 SZi = 2 ∙
5 = 10
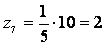
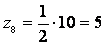
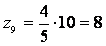
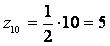
Так как
zmin
= 23, то принимая общий множитель12, имеем:
z7
= 24
z8 = 96
z9
= 60
z10 = 60
Для группы передач
i6
– i7
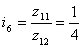 ai + bi = 1+4 = 5
ai + bi = 1+4 = 5
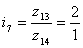 ai + bi = 2+1 = 3 SZi = 3 ∙
5 = 15
ai + bi = 2+1 = 3 SZi = 3 ∙
5 = 15
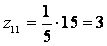
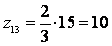
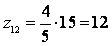
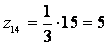
Так как
zmin
≥ 24 для данной группы передач, то принимаем общий множитель 8, имеем:
Z11
= 24
z12 = 96
z13
= 80
z14 = 40
Для передач
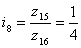 z15
= 24
z16 = 96.
z15
= 24
z16 = 96.
Для передач
 z17
= 25
z18 = 50.
z17
= 25
z18 = 50.
После подбора чисел зубьев всех шестерен проверяем отклонение
расчетных частот вращения шпинделя от теоретических. Для этого достаточно, чтобы
относительная величина общего передаточного отношения кинематической цепи
привода не выходила за пределы:
∆i
= ∆i1
+ ∆i2
+ … + ∆im
= 10(φ
- 1)% = 2,6%.
Так как передаточное отношение
ip.п.
ременной передачи можно подобрать точно, то считаем для нее ∆ip.п.
= 0.
Расчет относительных
погрешностей частных передаточных отношений сводим в таблице 7.10.
Таблица 7.10
|
Передаточное отношение |
Табличное |
Расчетное |
Относительная погрешность |
|
1 |
2 |
3 |
4 |
|
ip.п. |
0,690 |
0,690 |
|
|
i1 |
0,397 |
0,400 |
+0,75 |
|
i2 |
0,500 |
0,500 |
0 |
|
i3 |
0,631 |
0,628 |
-0,47 |
|
i4 |
0,250 |
0,250 |
0 |
|
i5 |
1,000 |
1,000 |
0 |
|
i6 |
0,250 |
0,250 |
0 |
|
i7 |
2,000 |
2,000 |
0 |
|
i8 |
0,250 |
0,250 |
0 |
|
i9 |
2,000 |
2,000 |
0 |
|
Общая относительная
погрешность передаточного отношения для каждой частоты вращения шпинделя:
∆i1
= 0 + 0 + 0 + 0,75 = +0,75 < ± 2,6
∆i2
= 0 + 0 + 0 + 0 = 0 < ± 2,6
∆i3
= 0 + 0 + 0 - 0,47 = -0,47 < ± 2,6
∆i4
= 0 + 0 + 0 + 0,75 = +0,75 < ± 2,6
∆i5
= 0 + 0 + 0 + 0 = 0 < ± 2,6
∆i6
= 0 + 0 + 0 - 0,47 = -0,47 < ± 2,6
∆i7
= 0 + 0 + 0 + 0,75 = +0,75 < ± 2,6
∆i8
= 0 + 0 + 0 + 0 = 0 < ± 2,6
∆i9
= 0 + 0 + 0 - 0,47 = -0,47 < ± 2,6
∆i10
= 0 + 0 + 0 + 0,75 = +0,75 < ± 2,6
∆i11
= 0 + 0 + 0 + 0 = 0 < ± 2,6
∆i12
= 0 + 0 + 0 - 0,47 = -0,47 < ± 2,6
∆i13
= 0 + 0 + 0 + 0,75 = +0,75 < ± 2,6
∆i14
= 0 + 0 + 0 + 0 = 0 < ± 2,6
∆i15
= 0 + 0 + 0 - 0,47 = -0,47 < ± 2,6
∆i16
= 0 + 0 + 0 + 0,75 = +0,75 < ± 2,6
∆i17
= 0 + 0 + 0 + 0 = 0 < ± 2,6
∆i18
= 0 + 0 + 0 - 0,47 = -0,47 < ± 2,6
∆i19
= 0 + 0 + 0 + 0,75
= +0,75 < ± 2,6
∆i20
= 0 + 0 + 0 + 0 = 0 < ± 2,6
∆i21
= 0 + 0 + 0 + 0,75 = +0,75 < ± 2,6
∆i22
= 0 + 0 + 0 + 0 = 0 < ± 2,6
∆i23
= 0 + 0 + 0 - 0,47 = -0,47 < ± 2,6
∆i24
= 0 + 0 + 0 + 0,75 = +0,75 < ± 2,6
∆i25
= 0 + 0 + 0 + 0 = 0 < ± 2,6
∆i26
= 0 + 0 + 0 - 0,47 = -0,47 < ± 2,6
Как следует из приведенных расчетов ∆ii,
числа зубьев колес подобраны правильно и фактические частоты вращения шпинделя
не выходят за пределы допуска табличных.
|